Теорема Гаусса для домохозяек
Начав преподавать Теоретические основы электротехники в колледже, столкнулся с тем, что учащимся трудно усвоить такие понятия, как напряженность и потенциал. Я и сам обучаясь в техникуме не очень хорошо понимал зачем эти величины нужны. С напряжением всё понятно: батарейку в 4,5 вольта можно лизнуть языком: щиплет. 220 вольт долбает по полной. И сила тока легко укладывается в голове: сильный ток плавит электроды в сварочном аппарате, слабый — едва улавливается точными приборами и нуждается в усилителе. Ну и сопротивление наглядно работает — как водопроводный кран: чем меньше «просвет», тем слабее через него течет (ток или вода). А вот напряженность электрического поля как понять?
Полистав старинные и современные учебники, в т.ч. англоязычные, я нашел в них большой методологический просчет. Все они начинают излагать теорию электрического поля с закона Кулона, тогда как гораздо проще объяснить его (поля) основополагающие характеристики на основании теоремы Га́усса. А вот, кстати, и он:

Прежде чем начать разговор об этой теореме — пара слов о том, чем неудобен для усвоения закон Кулона. Выведенная из него величина напряженности выглядит вот как:
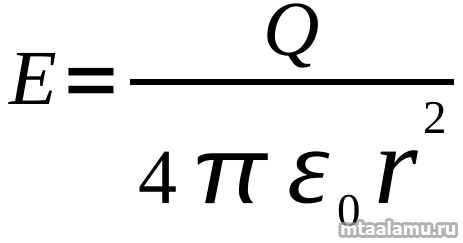
Q — заряд, r — расстояние от заряда до точки, напряженность которой нас интересует. Устрашающая формула, не правда ли? Почему r в квадрате, откуда взялось число пи, да еще учетверенное, если расстояние меряется по прямой, а не по окружности? Преподаватели иной раз сами не могут ответить на этот вопрос и преподносят закон Кулона как данность: мол, дяденька Кулон трудился, опыты ставил, нашел вот для вас, балбесов, формулу, а от вас только одно требуется: вызубрить ее и правильно ответить на экзамене.
Через несколько страниц после формулы Кулона в учебниках обычно пишут про теоретические разработки Гаусса и приводят его выводы, причем часто без доказательств, мол, не вашего ума дело (сам видел такой учебник, точнее говоря он у меня дома есть). Между тем теорема Гаусса не сложнее, чем процесс дележки кулька конфет между детишками детского сада. Попробую это доказать.
Прежде пара слов о самом Иоганне Карле Фри́дрихе Га́уссе. Это был матерый человечище, выходец из бедной крестьянской семьи, который, подобно нашему Ломоносову, стал одним из величайших светил науки. Он доказывал такие теоремы, что ведущие академии Европы стояли в очередь на право записать его к себе в почетные члены. Например, однажды Гаусс путем всего лишь умственных вычислений нашел пропавшую из поля зрения астрономов планету и точно указал область неба, где ее следует искать. Вот иллюстрация, на которой мозг Гаусса изображен в сравнении с мозгом простого человека. Количество извилин впечатляет.
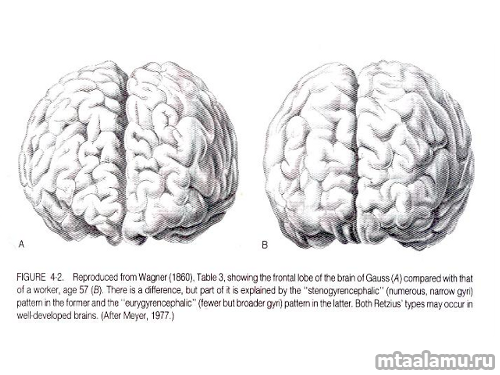
Тот, кто активно пользуется Фотошопом, несомненно сталкивался с гауссовым размытием, позволяющим сделать картинку «мягче». Нас, однако, интересует только теорема Гаусса, касающаяся электрического поля вокруг неподвижного заряда (электричеством ученый занимался уже на склоне лет).
Итак, представим себе неподвижное электрически заряженное тело, например, расческу, которой провели по сухим волосам, хотя гораздо удобнее представить себе заряженный шарик, именно он используется в дальнейших рассуждениях. На расстоянии R1 от шарика представим сферу, каждую точку которой представим тоже в виде маленького шарика фиксированного размера и заряда. Еще одну сферу изобразим на несколько большем расстоянии от заряженного тела — R2. Ее поверхность состоит из таких же (по размеру и заряду) эталонных шариков, что и первая.
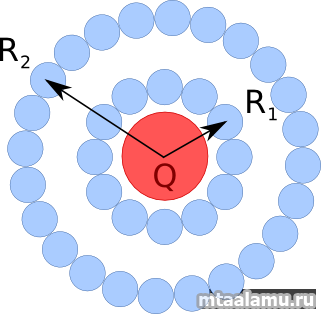
Теперь от каждой сферы оставим по одной точке, в которую «спрессуем» все шарики соответствующей сферы. При этом их заряды сложатся.
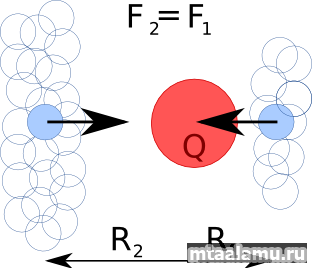
Малая сфера состоит из меньшего количества шариков, но зато расстояние от нее до заряженного тела было ближе и сила притяжения, действовавшая на каждый шарик, была сильнее, чем для большой. Сила воздействия на каждый шарик большой сферы была меньше за счет большей удаленности от заряженного тела, но зато шариков было больше. На какую из «спрессованых» точек — принадлежащую большей или меньшей сфере — действует со стороны заряженного тела большая сила? Какой из факторов — близость к заряженному телу или количество шариков — окажет большее влияние на величину этой силы? Опыты Кулона и размышления Гаусса свидетельствуют о том, что силы эти окажутся одинаковыми и будут зависеть только от величины самого заряда и среды, в которой действует электрическое поле:
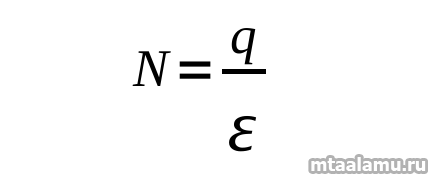
где N — некая силовая величина, характеризующая воздействие заряда на ту или иную сферу, состоящую из наших эталонных шариков. Эпсилон в знаменателе — характеристика вещества, в котором действует электрическое поле (в воздухе оно сильнее, в воде слабее и т.д.), ну и еще система единиц измерения в этом же коэффициенте заложена.
Ну, а как найти силу, действующую на каждый отдельный бесконечно малый шарик, которая как раз и называется напряженностью электрического поля? Очень просто, нужно разделить N на площадь поверхности сферы, которая, как известно из школьного курса геометрии, равна 4 Пи умноженное на радиус в квадрате. Вот откуда взялся знаменатель в формуле закона Кулона! Теперь становится понятным и смысл более сложных формул, открывающих дорогу к понятиям потенциала, напряжения, закону Ома и т.п.
Sapienti sat.
Полистав старинные и современные учебники, в т.ч. англоязычные, я нашел в них большой методологический просчет. Все они начинают излагать теорию электрического поля с закона Кулона, тогда как гораздо проще объяснить его (поля) основополагающие характеристики на основании теоремы Га́усса. А вот, кстати, и он:

Прежде чем начать разговор об этой теореме — пара слов о том, чем неудобен для усвоения закон Кулона. Выведенная из него величина напряженности выглядит вот как:
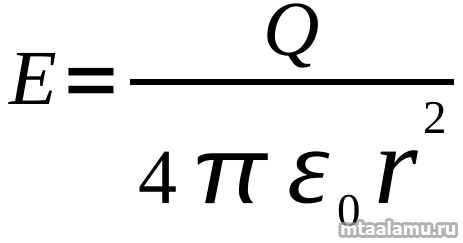
Q — заряд, r — расстояние от заряда до точки, напряженность которой нас интересует. Устрашающая формула, не правда ли? Почему r в квадрате, откуда взялось число пи, да еще учетверенное, если расстояние меряется по прямой, а не по окружности? Преподаватели иной раз сами не могут ответить на этот вопрос и преподносят закон Кулона как данность: мол, дяденька Кулон трудился, опыты ставил, нашел вот для вас, балбесов, формулу, а от вас только одно требуется: вызубрить ее и правильно ответить на экзамене.
Через несколько страниц после формулы Кулона в учебниках обычно пишут про теоретические разработки Гаусса и приводят его выводы, причем часто без доказательств, мол, не вашего ума дело (сам видел такой учебник, точнее говоря он у меня дома есть). Между тем теорема Гаусса не сложнее, чем процесс дележки кулька конфет между детишками детского сада. Попробую это доказать.
Прежде пара слов о самом Иоганне Карле Фри́дрихе Га́уссе. Это был матерый человечище, выходец из бедной крестьянской семьи, который, подобно нашему Ломоносову, стал одним из величайших светил науки. Он доказывал такие теоремы, что ведущие академии Европы стояли в очередь на право записать его к себе в почетные члены. Например, однажды Гаусс путем всего лишь умственных вычислений нашел пропавшую из поля зрения астрономов планету и точно указал область неба, где ее следует искать. Вот иллюстрация, на которой мозг Гаусса изображен в сравнении с мозгом простого человека. Количество извилин впечатляет.

Тот, кто активно пользуется Фотошопом, несомненно сталкивался с гауссовым размытием, позволяющим сделать картинку «мягче». Нас, однако, интересует только теорема Гаусса, касающаяся электрического поля вокруг неподвижного заряда (электричеством ученый занимался уже на склоне лет).
Итак, представим себе неподвижное электрически заряженное тело, например, расческу, которой провели по сухим волосам, хотя гораздо удобнее представить себе заряженный шарик, именно он используется в дальнейших рассуждениях. На расстоянии R1 от шарика представим сферу, каждую точку которой представим тоже в виде маленького шарика фиксированного размера и заряда. Еще одну сферу изобразим на несколько большем расстоянии от заряженного тела — R2. Ее поверхность состоит из таких же (по размеру и заряду) эталонных шариков, что и первая.

Теперь от каждой сферы оставим по одной точке, в которую «спрессуем» все шарики соответствующей сферы. При этом их заряды сложатся.

Малая сфера состоит из меньшего количества шариков, но зато расстояние от нее до заряженного тела было ближе и сила притяжения, действовавшая на каждый шарик, была сильнее, чем для большой. Сила воздействия на каждый шарик большой сферы была меньше за счет большей удаленности от заряженного тела, но зато шариков было больше. На какую из «спрессованых» точек — принадлежащую большей или меньшей сфере — действует со стороны заряженного тела большая сила? Какой из факторов — близость к заряженному телу или количество шариков — окажет большее влияние на величину этой силы? Опыты Кулона и размышления Гаусса свидетельствуют о том, что силы эти окажутся одинаковыми и будут зависеть только от величины самого заряда и среды, в которой действует электрическое поле:
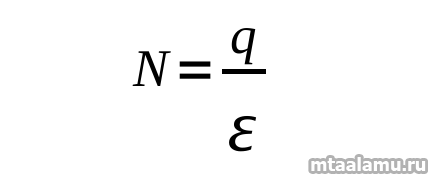
где N — некая силовая величина, характеризующая воздействие заряда на ту или иную сферу, состоящую из наших эталонных шариков. Эпсилон в знаменателе — характеристика вещества, в котором действует электрическое поле (в воздухе оно сильнее, в воде слабее и т.д.), ну и еще система единиц измерения в этом же коэффициенте заложена.
Ну, а как найти силу, действующую на каждый отдельный бесконечно малый шарик, которая как раз и называется напряженностью электрического поля? Очень просто, нужно разделить N на площадь поверхности сферы, которая, как известно из школьного курса геометрии, равна 4 Пи умноженное на радиус в квадрате. Вот откуда взялся знаменатель в формуле закона Кулона! Теперь становится понятным и смысл более сложных формул, открывающих дорогу к понятиям потенциала, напряжения, закону Ома и т.п.
Sapienti sat.

Комментарии (9)
RSS свернуть / развернутьВот к примеру Напряженность поля радиосигнала в точке приема от расстояния и Мощности излучения.
Несуразности компенсирует Коеффициент.
E = Коеффициент. х Pизлучен. / 4 Пи R(квадр)
Подробнее в это разбирался Максвелл.
В институтах этим занимается предмет Теория Общего Электричества (ТОЭ).
Markony
yababay
ddclient
ahmetzyanov_d
Сегодня проводил испытания этого способа объяснения «на живых людях». После этого задачи на напряженность стали решаться с бо'льшим пониманием.
yababay
Ну а по существу — у Вас, похоже, ошибка в размышлениях: Вы приравниваете F1 и F2, а это неверно в том смысле, что у разноудаленных от заряда (как источника электростатического поля) точек пространства напряженность будет различной. Ведь квадрат радиуса в формуле напряженности — это отнюдь не радиус пробного точечного заряда (который, по определению, ничтожно мал, и настолько, что им вообще можно пренебречь), а именно радиус сферы, центр которой является зарядом Q (повторюсь, являющимся источником поля), а пробный заряд q+ лежит на поверхности данной сферы. Так вот расстояние от центра сферы до зарядика q+ — это и есть радиус r. Поэтому чем дальше от Q, тем меньше напряженность. Как говорится, Солнце тоже не выбирает, на кого ему светить сильнее, а на кого — слабее, но чем дальше от светила, тем холодней.
Texas
Честно говоря, так давно писал эту статью, что уже не очень хорошо помню ход собственных рассуждений, да и электротехнику давно не преподаю.
Пожалуй, здесь с толку сбивает фраза «при этом их заряды сложатся», ведь речь идет не о зарядах (ими шарики в самом начале рассуждения и не обладают), а об абстрактной способности шариков притягиваться к заряду Q. Чем дальше от него — тем меньшее притяжение испытывает каждый шарик. Если же мы хотим узнать во сколько раз меньшее притяжение шарик большой сферы испытывает, по сравнению с шариком малой сферы, то должны сопоставить площади этих сфер и учесть свойства окружающей эту систему среды.
yababay
Ну я бы даже сказал, что и складывать-то вообщем ничего и не надо. Все дело-то как раз в том, что этот пробный шарик q+ своим ничтожно малым полем практически никак не влияет на среду, и будь их хоть миллион — они и в этом случае ничего (в плане заряда) не представляют.
При этом, конечно, чем дальше q от Q, тем меньше притяжение, ну или отталкивание (вот, Вы и сами это признали); тем меньше напряженность. Конечно, и диэлектрическую проницаемость среды нужно учитывать. Но, кстати, площади сфер можно и не сопоставлять — они «автоматически» будут разными, в зависимости от разницы между радиус — векторами. Поэтому достаточно учесть именно разницу в значениях r — и дело в шляпе.
С Наступающим Вас и успехов в Новом году!
Texas
yababay
Только зарегистрированные и авторизованные пользователи могут оставлять комментарии.