Sage: строим полиномы Цернике
В данном топике забавы ради и понимания для мы построим в системе Sage полиномы Цернике, которые даны в виде функций в полярных координатах.
Форма и порядок полиномов Цернике (взято из книги Л.И. Балашевича Клиническая корнеотопография и аберрометрия):
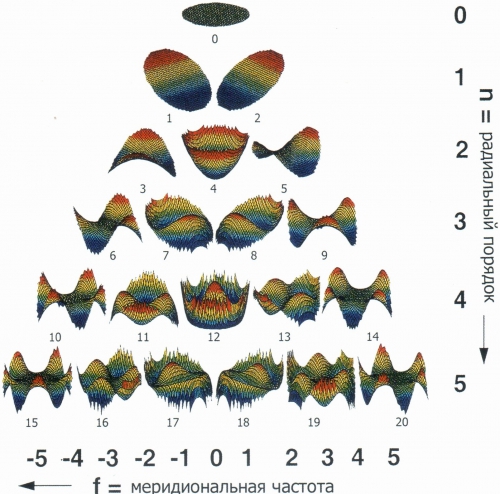
По данной таблице можно определить номер полинома:
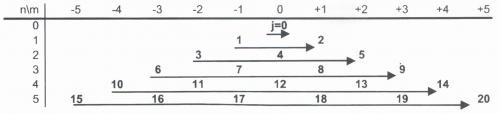
И формулы разных полиномов в полярной системе координат:
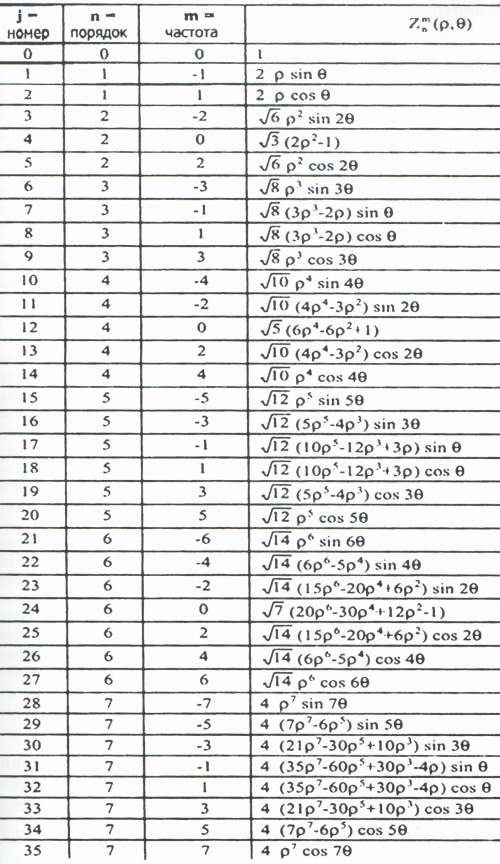
Итак, построим в системе Sage некоторые полиномы. О Sage я писал ранее тут.
Запускаем Sage в консоли из графического режима. Это важно, т.к. для вывода графиков используется графическая утилита Jmol — тут и повращать можно и сделать скриншоты и т.п.
Для начала в консоли Sage декларируем переменные:
Затем создаем трансформацию для полярных координат:
Строим 1й наш график:
После выполнения данной комманды будет открыто окно jmol:

Построим полином №3 (астигматизм):
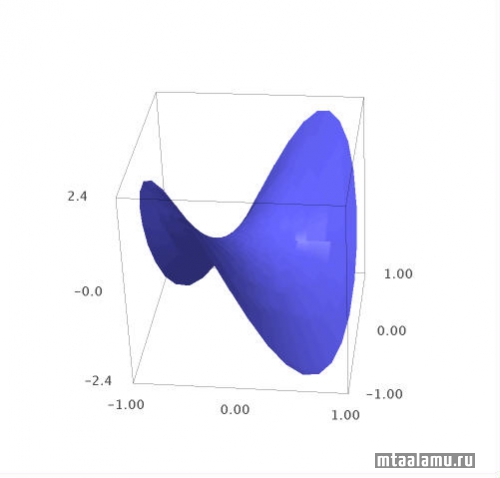
Построим полином №7 (кома):
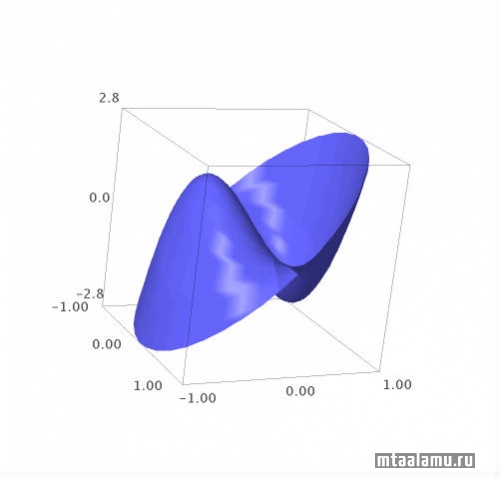
И, например, 19й:

Вот так все просто!
Форма и порядок полиномов Цернике (взято из книги Л.И. Балашевича Клиническая корнеотопография и аберрометрия):

По данной таблице можно определить номер полинома:

И формулы разных полиномов в полярной системе координат:

Итак, построим в системе Sage некоторые полиномы. О Sage я писал ранее тут.
Запускаем Sage в консоли из графического режима. Это важно, т.к. для вывода графиков используется графическая утилита Jmol — тут и повращать можно и сделать скриншоты и т.п.
Для начала в консоли Sage декларируем переменные:
sage: r, theta, z = var('r theta z')Затем создаем трансформацию для полярных координат:
sage: T = Cylindrical('height', ['radius', 'azimuth'])
sage: T.transform(radius=r, azimuth=theta, height=z)Строим 1й наш график:
sage: plot3d(2 * r * sin (theta), (r, 0, 1), (theta, 0, 2*pi), transformation=T)После выполнения данной комманды будет открыто окно jmol:

Построим полином №3 (астигматизм):
sage: plot3d(sqrt(6) * r^2 * sin (2*theta), (r, 0, 1), (theta, 0, 2*pi), transformation=T)
Построим полином №7 (кома):
sage: plot3d(sqrt( 8 ) * (3 * r^3 - 2 * r) * sin (theta), (r, 0, 1), (theta, 0, 2*pi), transformation=T)
И, например, 19й:
sage: plot3d(sqrt(12) * (5 * r^5 - 4 * r^3) * cos (3*theta), (r, 0, 1), (theta, 0, 2*pi), transformation=T)
Вот так все просто!
- —
- 16 июля 2012, 13:08

Комментарии (2)
RSS свернуть / развернутьспасибо за этот пост
sagax
Sergei_T
Только зарегистрированные и авторизованные пользователи могут оставлять комментарии.