Сегодня я покажу небольшой пример решения уравнения с помощью open source системы Sage. Sage позиционируется как открытая альтернатива Magma, Maple, Mathematica, MATLAB. Система может работать в режиме интерпретатора, открывать готовые файлы с выражениями, использоваться в коде на Python. Кроме того, Sage обладает веб интерфейсом, позволяющим хранить так называемые «рабочие листы» с расчетами (worksheets):



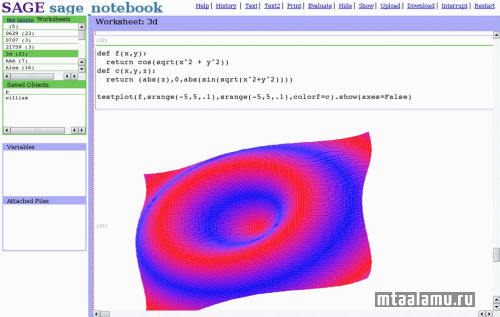
Пример онлайн интерфейса можно посмотреть здесь.

Вообще, система может работать на нескольких платформах, но я использовал OpenSUSE 11.4. Готовых пакетов под мой дистрибутив не было, были только для Fedora и Ubuntu, так что пришлось собирать из исходного кода (около 500 Мб). Для сборки нужно лишь выполнить в директории исходников команду make (должен быть установлен gcc и заголовочные файлы python). К слову на моем слабеньком нетбуке на сборку ушло около 15 часов.

Стоило ли? Стоило!

Привожу небольшой пример практического применения. Если не вдаваться в предметную область (а про нее здесь можно почитать здесь или копия здесь), то нужно было решить несложное, но очень громоздкое уравнение. Есть вот такой набор выражений:



Обозначения я упростил, post = APostRx, iol = IOLe, l = ALo.
Данные K (k), L (l), IOL (iol), V (v) — взяты из примера в статье.

Сохраняем в файл с расширением .sage вот такой код:

var ('a, b, c, iol, x, l, k, v, post, elp')
eq1 = 1336/(1000/(1000/post-v)+k)==x
eq2 = a==iol
eq3 = b==-1*iol*(l+x)
eq4 = c==1336*(l-x)+iol*x*l
eq5 = elp==(-1*b-sqrt(b*b-4*a*c))/(2*a)

solns = solve([eq1,eq2,eq3,eq4,eq5,iol==22.5,l==22.48,k==46.685*0.98765431,v==12,post==-0.5],a,b,c,iol,x,l,k,v,post,elp,solution_dict=True)
print [[s[elp].n(30)] for s in solns]

solns = solve([eq1,eq2,eq3,eq4,eq5,iol==22.5,l==22.48,k==46.685*0.98765431,v==12,elp==5.4891738],a,b,c,iol,x,l,k,v,post,elp,solution_dict=True)
print [[s[post].n(30)] for s in solns]

В первый заход мы считаем параметр elp исходя из заданных исходных данных (iol, k, l, v, post), что не сложно, но вот во второй заход мы наоборот, зная elp получаем значение post, что вручную сделать довольно сложно. Решает уравнение команда solve, нужно только задать исходные данные.

Запускаем Sage в коммандной строке:

./sage

Вводим:

attach calc.sage

Этой командой мы привязываем созданный .sage файл (в моем случае calc.sage) к интерпретатору. При изменении файла достточно нажать на Enter в интерпретаторе Sage и все будет пересчитано:

sage: 
[[5.4891738]]
[[-0.50000008]]

Первый результат — это прямой расчет, второй — зная переменную elp (5.489) определение переменной post.

Кстати, у Sage есть документация на русском языке:
www.sagemath.org/ru/html/tutorial/