Понадобилось для простых вычислений, думал все будет просто, но не тут то было, оказывается за многие годы все порядком забылось.
И вот оно чудо — www.math-pr.com/index.html

Пример перемножения матриц

Выбираем параметры матрицы



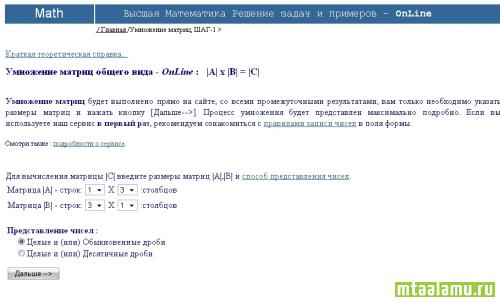
Вводим значения



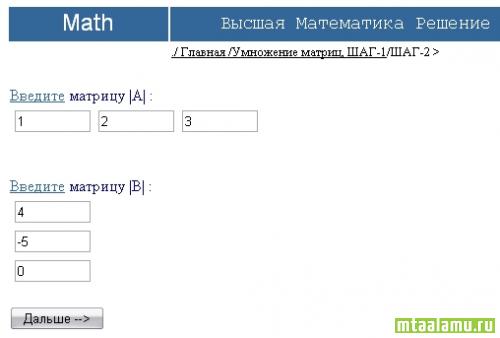
И вуаля



Более сложная задача
Задача:
Найти ранг матрицы |A|:
1; 1; 1; 2; 1;
1; (-2); (-3); 1; -1;
2; (-1); (-2); 3; 0.

Как известно, ранг матрицы не изменяется:
a) при перестановке двух строк;
б) при умножении одной строки на число отличное от нуля;
в) при прибавлении (вычитании) некоторой строки умноженной на любое число к другой строке;
г) при транспонировании.

Из последнего следует, что описанные выше правила справедливы и для столбцов.

Для нахождение ранга матрицы, преобразуем исходную матрицу в трапециевидную равного ранга. Для этого воспользуемся описанными выше правилами. При этом стремимся, чтобы все элементы стоящие ниже главной диагонали были равны нулю, а все элементы стоящие на главной диагонали были отличны от нуля (возможно кроме последних, стоящих в полностью нулевых строках).

Шаг:1
Вычтем из строки 2 строку 1 умноженную на a(2,1)=1
Вычитаемая строка:
1; 1; 1; 2; 1.

Модифицированная матрица:
1; 1; 1; 2; 1;
0; (-3); (-4); (-1); (-2);
2; (-1); (-2); ;3 0.

Шаг:2
Вычтем из строки 3 строку 1 умноженную на a(3,1)=2
Вычитаемая строка:
2; 2; 2; 4; 2.

Модифицированная матрица:
1; 1; 1; 2; 1;
0; (-3); (-4); (-1); (-2);
0; (-3); (-4); (-1); (-2).

Шаг:3
Разделим строку 2 на a(2,2)=-3
Получим матрицу:
1; 1; 1; 2; 1;
0; 1; (4/3); (1/3); (2/3);
0; (-3); (-4); (-1); (-2).

Шаг:4
Вычтем из строки 3 строку 2 умноженную на a(3,2)=-3
Вычитаемая строка:
0; (-3); (-4); (-1); (-2).

Модифицированная матрица:
1; 1; 1; 2; 1;
0; 1; 4/3; 1/3; 2/3;
0; 0; 0; 0; 0.

Требуемый вид матрицы получен и ее ранг совпадает с рангом исходной.

Проанализируем последнюю матрицу, в ней легко выделить невырожденную квадратную подматрицу (минор) порядка 2. Этот минор располагается с 1-й по 2-ю строку и с 1-го по 2-й столбец (см. ниже).

Минор 2-го порядка:
1; 1;
0; 1.

Данный минор невырожденный (его определитель не равен нулю) т.к. определитель треугольной матрицы равен произведению диагональных элементов. Кроме того, из конечной матрицы нельзя выделить невырожденную подматрицу порядка больше чем 2, следовательно, ранг матрицы |A| равен 2

Ответ: rang|А|=2

Решение не проверял! Осталось на моей совести